CSAW’18 CTF Qualification: Take an L

Challenge details

Event	Challenge	Category	Points	Solves
CSAW’18 CTF Qualification	Take an L	Misc (Prog)	200	192

Download: description.pdf - md5: 79b489dcacb5b0002ed34a270bdfe184

Description

Fill the grid with L’s but avoid the marked spot for the W

nc misc.chal.csaw.io 9000

The origin is at (0,0) on the top left

TL;DR

This was a programming challenge looking like polyominos puzzle. To solve the challenge, I found a recursiv algorithm for the given problem: https://www.geeksforgeeks.org/divide-and-conquer-set-6-tiling-problem/

Methology

Explain as an algorithm problem

First thing to do was reading the description an think about the mathematic/programming problem we had. By running the challeng we got the following:

nc misc.chal.csaw.io 9000

each L shaped block should be sent in its 
own line in a comma separated list
eg: (a,b),(a,c),(d,c)

grid dimensions 64x64
marked block: (18, 3)

I made few search about “puzzle” such as Tetris I found the “polyomino” wikipedia page. Our polyominos were “trominos”, I decided to search for a polyomino/tromino solver online.

Geek for Geek

As usual with algorithmic problems, I looked at the website “GeeksForGeeks”. With a litle research on google, I found exactly what I needed: a L-tromino solver for a given grid with a “black” (filled) cell.

Explanation of recursiv algorithm

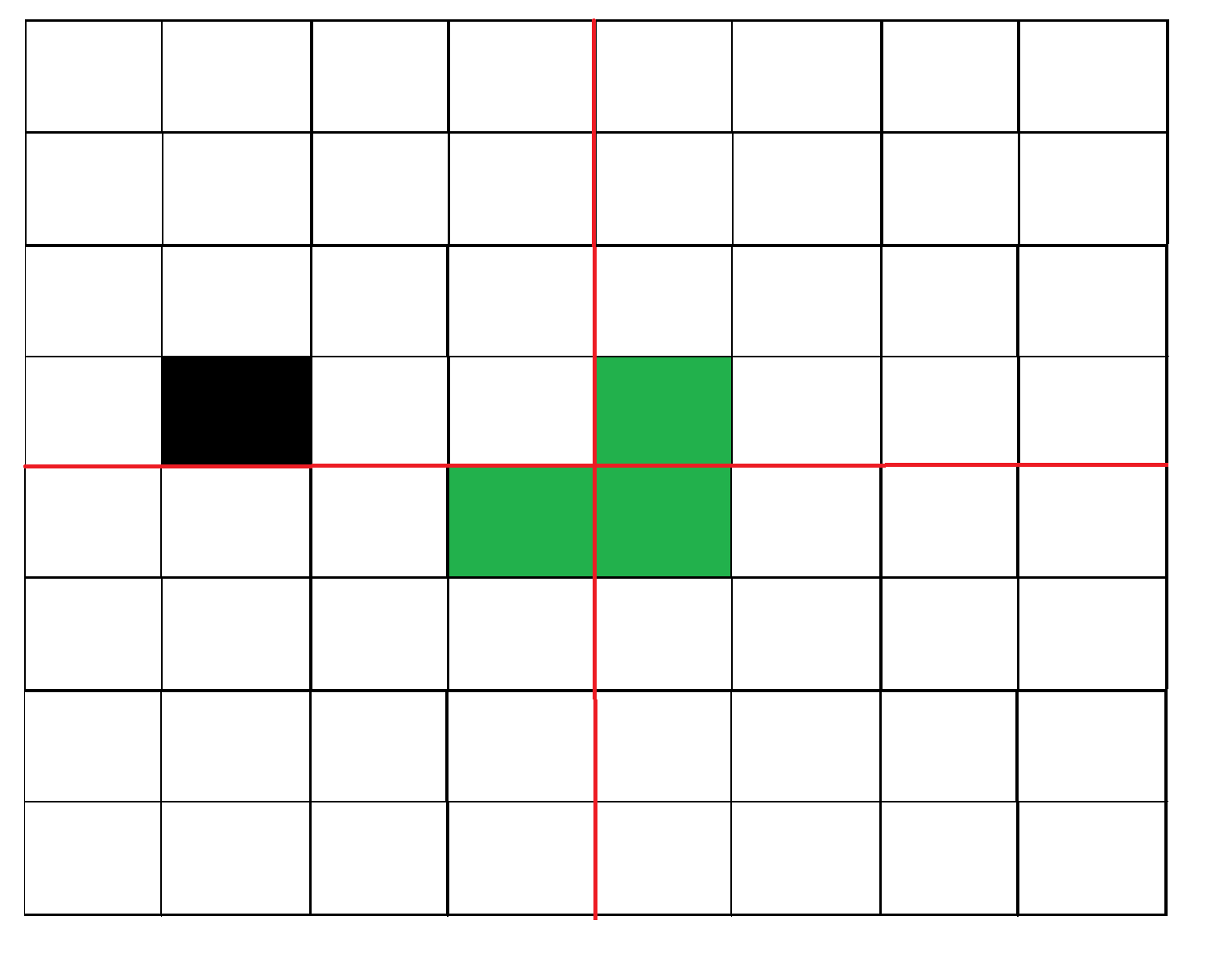
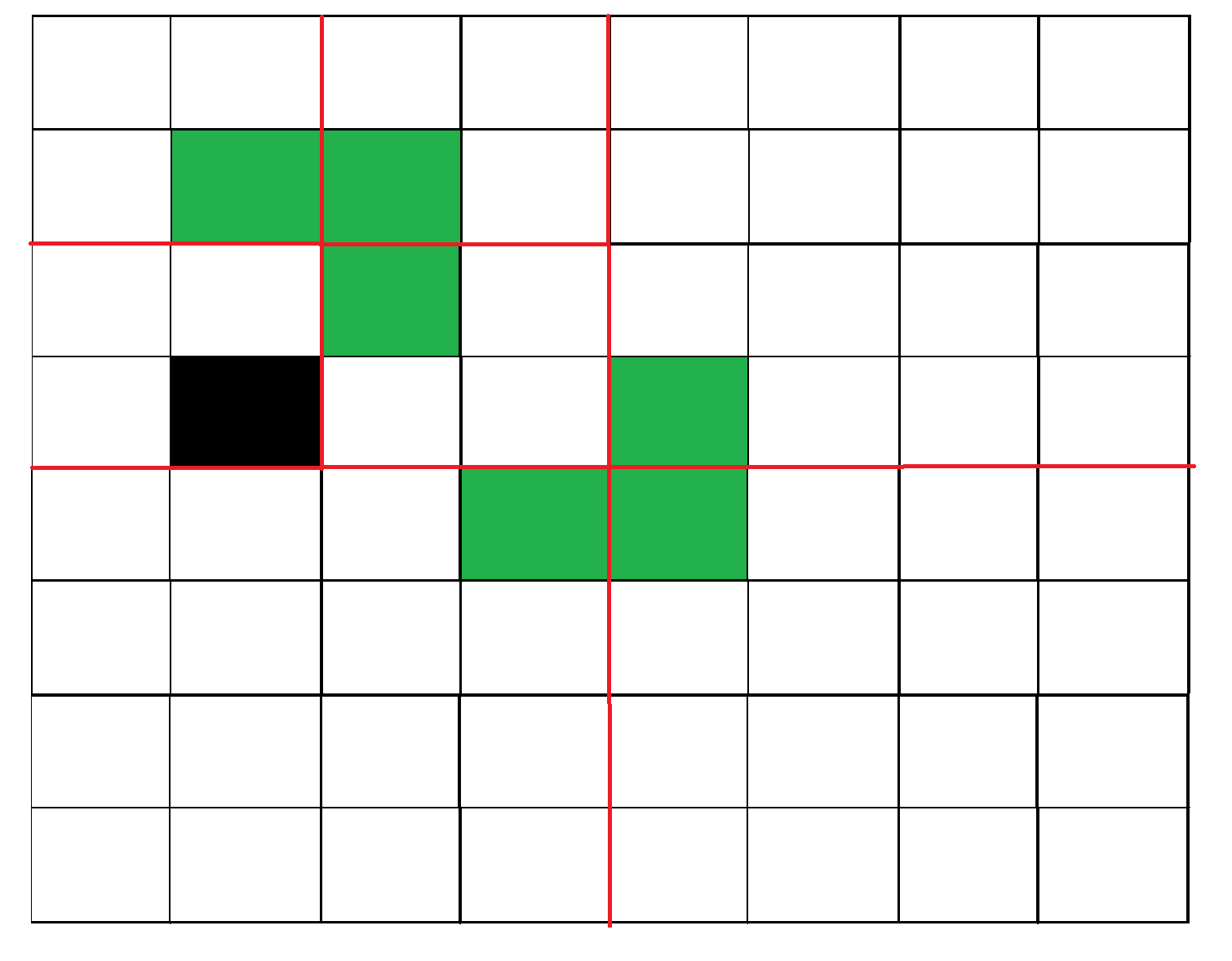
The algorithm I decided to used was recursiv. The algorithm execute the following process: we put an “L” (L-tromino) on the middle of the grid, then we split the grid into subgrid and do the same process for each subgrid. The recursiv function stop when the grid is same size as our “L” (2*2). To fulfill the grid, the missing square of our “L” must be oriented in the direction of the occupied cell of the grid.

Here are a representation of the 2 firsts step for a 8*8 grid:

Step 1:

Step 2:

Code for a 64*64 grid

As 64 is a multiple of 4, we can use our algorithm. I decided to implement it in python, here is my code (not the best one I wrote…):

# -*- coding:utf-8 -*-
from pwn import *
 
HOST = "misc.chal.csaw.io"
PORT = 9000

r = remote(HOST, PORT)

def send(c):
    """ Send new 'L' to server """
    print(c)
    r.sendline(c)


rec =  r.recvuntil("marked block: ")
print(rec)
black = eval(r.recvuntil("\n").strip())
print("Black cell: "+str(black))

n = 64 # Array Size
a = [[' ' for x in range(n)] for y in range(n)] # Init empty array
a[black[1]][black[0]] = "@" # Black case (filled one) (given when started)


def pgrille():
    """ Save current Grid to logs """
    out = ""
    out += "-"*n
    out += "\n"
    for l in a:
        out += str(''.join([x for x in l]))+"\n"
    out += "-"*n
    with open("logs","a+") as fi:
        fi.write(out+"\n\n\n")


def getBlack(a,x_start,y_start,x_end,y_end):
    """ Get position of "black" square of array / sub array """
    for j in range(y_start,y_end+1):
        for i in range(x_start,x_end+1):
            if a[j][i] == "o" or a[j][i] == "@":
                return i,j
    return None,None # Should not happen


def Tile(a,x_start,y_start,x_end,y_end):
    """ Recursive function, put an L in the middle and act recursivly.
    'L' are represented with 3*'o'. """
    xcenter_left = x_start+((x_end-x_start)/2)
    xcenter_right = xcenter_left+1
    ycenter_top = y_start+((y_end-y_start)/2)
    ycenter_bottom = ycenter_top+1
    
    xBlack,yBlack = getBlack(a,x_start,y_start,x_end,y_end)
    
    # Define "L" direction/orientation and send new triangle
    if xBlack <= xcenter_left: # Black cell on the left
        if yBlack <= ycenter_top: # Black cell on the top
            a[ycenter_top][xcenter_right] = "o"
            a[ycenter_bottom][xcenter_right] = "o"
            a[ycenter_bottom][xcenter_left] = "o"
            send("("+str(xcenter_right)+","+str(ycenter_top)+"),("+str(xcenter_right)+","+str(ycenter_bottom)+"),("+str(xcenter_left)+","+str(ycenter_bottom)+")")
        else: # Black cell on the bottom
            a[ycenter_top][xcenter_left] = "o"
            a[ycenter_top][xcenter_right] = "o"
            a[ycenter_bottom][xcenter_right] = "o"
            send("("+str(xcenter_left)+","+str(ycenter_top)+"),("+str(xcenter_right)+","+str(ycenter_top)+"),("+str(xcenter_right)+","+str(ycenter_bottom)+")")
    else: # Black cell on the right
        if yBlack <= ycenter_top: # Black cell on the top
            a[ycenter_top][xcenter_left] = "o"
            a[ycenter_bottom][xcenter_left] = "o"
            a[ycenter_bottom][xcenter_right] = "o"
            send("("+str(xcenter_left)+","+str(ycenter_top)+"),("+str(xcenter_left)+","+str(ycenter_bottom)+"),("+str(xcenter_right)+","+str(ycenter_bottom)+")")
        else: # Black cell is on the bottom
            a[ycenter_bottom][xcenter_left] = "o"
            a[ycenter_top][xcenter_left] = "o"
            a[ycenter_top][xcenter_right] = "o"
            send("("+str(xcenter_left)+","+str(ycenter_bottom)+"),("+str(xcenter_left)+","+str(ycenter_top)+"),("+str(xcenter_right)+","+str(ycenter_top)+")")
    
    pgrille() # Print in logs
    
    if abs(x_end-x_start) > 1: # If grid is big enough, go recursiv
        Tile(a,x_start,y_start,xcenter_left,ycenter_top)
        Tile(a,xcenter_right,y_start,x_end,ycenter_top)
        Tile(a,x_start,ycenter_bottom,xcenter_left,y_end)
        Tile(a,xcenter_right,ycenter_bottom,x_end,y_end)
    
Tile(a,0,0,len(a[0])-1,len(a)-1) # Start on full array
    
r.interactive() # Get shell

Flag

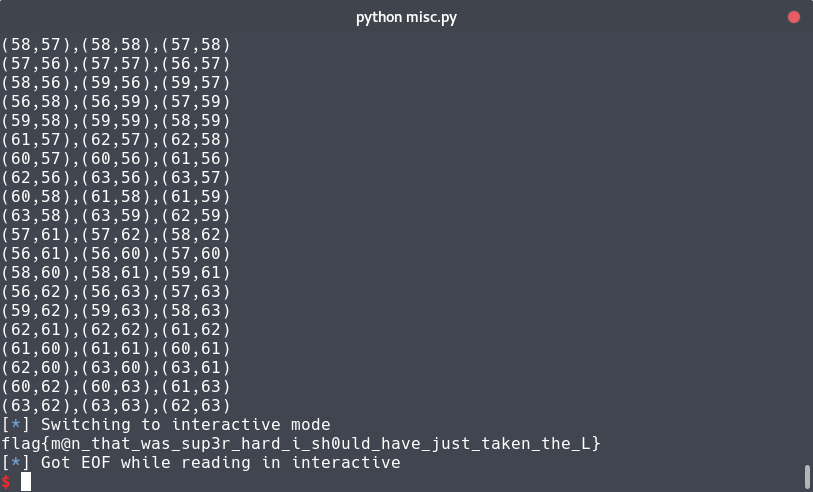
flag{m@n_that_was_sup3r_hard_i_sh0uld_have_just_taken_the_L}

Zeecka