Clutter

Description

Out of clutter, find simplicity.

A colleague of yours has sent you a program he developed and wants to challenge you.

Validate your access and give him the flag.

File: chall.

TL;DR

The binary has been obfuscated using a kind of VM-based code obfuscation technique. Describing the basic blocks and the dispatcher of the VM helps us to recover the control flow and understand the program logic. Then, we just have to pass some checks found during the analysis to reach the flag.

Reverse Engineering

The file we’re given is a x86_64 ELF executable:

# file chall
chall: ELF 64-bit LSB pie executable, x86-64, version 1 (SYSV), dynamically linked, interpreter /lib64/ld-linux-x86-64.so.2, for GNU/Linux 3.2.0, BuildID[sha1]=8ac41d198a50fb0cd4b9c2aff531540512f433f1, stripped

The binary is stripped so we won’t have any debug symbols.

Looking at the .rodata segment, we can see that there are not many strings, but some of them are referring to the flag output:

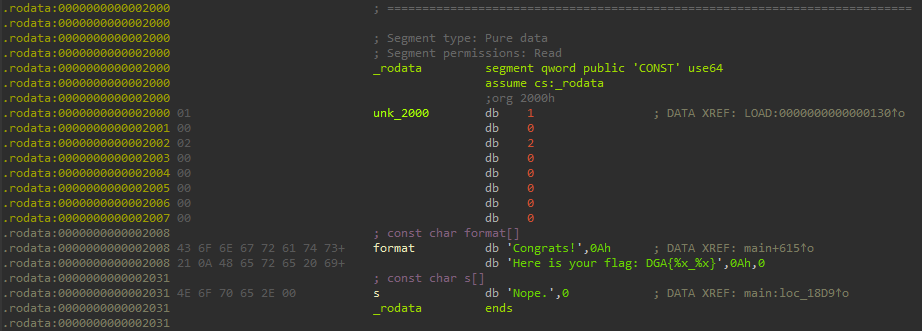
All these strings are used within the main function, let’s analyze it.

main function analysis

When opening the main function in IDA and switching to the graph disassembly view, we quickly see that the binary has been obfuscated:

A brief study of the graph shows that it’s a kind of VM-based logic obfuscation:

• we find a loop in which several blocks of instructions are aligned
• each of these blocks can be identified by its access condition (here the value of a specific variable)
• each block has a well-defined role and can be called several times during the program’s life cycle

This type of program usually uses virtual registers stored in a context that can also contain a virtual stack. This context is basically used to hold the program state between each basic blocks of the program, for example:

• a block A sets the values of two registers R0 and R1 (where R# represent virtual registers stored in a rw segment):

block A
mov r0, 1
mov r1, 3
end block

• a block B performs arithmetic operations:

block B
xor r0, r1
add r1, r0
end block

• a block C prints the value of R0:

block C
out r0
end block

An in-depth analysis of the internal logic of the VM allows us to identify some types of logical blocks:

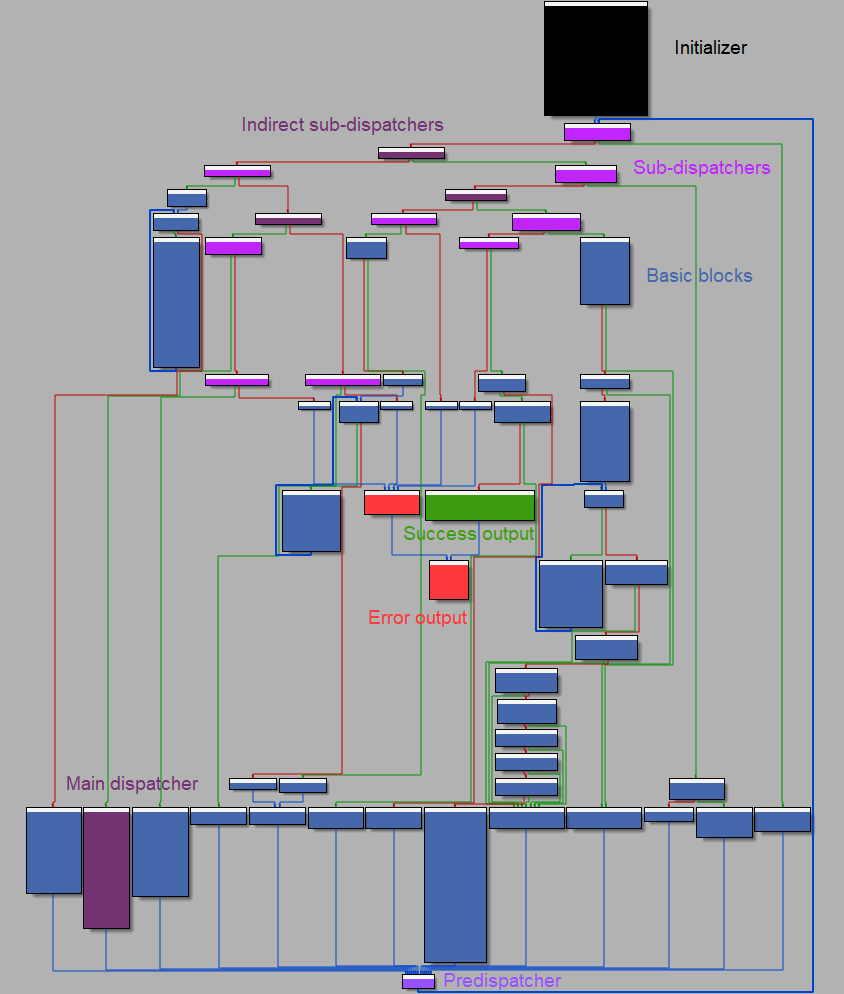
• The initializer block (also known as prologue) is used to load and define some variables of the VM context (stored in the .data segment).
• The basic blocks are used to handle the whole program logic and rely on the VM context to hold the results of arithmetic operations, I/O control, branches, etc.
• The sub-dispatchers blocks are used to jump to the VM basic blocks based on the current block_id value (which acts as a PC/IP register inside the VM).
• The main dispatcher is used to compute the next block_id value based on a control value (ctl). It’s worth noting that because it’s accessed via the sub-dispatchers, the main dispatcher is also a basic block and as such should be referenced at the end of each basic block.
• The success and error outputs are used to exit the program when something happens.

Basic block analysis

As we said earlier, each basic block has a well-defined role and can be called several times during the program life cycle. Let’s enumerate and describe these basic blocks:

Address	Block ID	Block name	Basic description
0x137D	0x6a09e667	DISPATCH_BLOCK	Define the next block_id based on the ctl variable value.
0x13EB	0x679dfce7	TRANSFORM_TABLE_BLOCK	Do some magic over a table stored in the context.
0x14FF	0x6df725a7	GET_USER_INPUT_BLOCK	Get the user input values in hexadecimal format (using the strtoul function).
0x156A	0x78b38527	STORE_USER_INPUT_BLOCK	Store the user input in some virtual registers of the context.
0x17B7	0x6ca7afa7	PREPARE_COUNTER_BLOCK	Define the initial value (9) of a counter (R10) in the context.
0x17D1	0x6ac7a3a7	XOR_REGISTERS_BLOCK	XOR all virtual registers from R9 to R0 with the previous one.
0x1841	0x66cbba27	DUMMY_JMP_DEC_COUNTER_BLOCK	Does nothing except jumping to the DEC_COUNTER_BLOCK.
0x184D	0x70b9d067	DEC_COUNTER_BLOCK	Decrement R10 and jump to R0 when R10 is equal to 0.
0x1881	0xdeadbeef	CHECK_FLAG_BLOCK	Check the last value of the table stored in the context (0xA3EFA1D) and print the flag.
0x18D9	0xdeaddead or any other invalid value for block_id.	INVALID_BLOCK	Exit the program.

Following this analysis, we notice several things:

• the LSBs of all these basic block identifiers end with 100111 in binary, except for the CHECK_FLAG_BLOCK and INVALID_BLOCK blocks, we can assume that these values can’ t be obtained from the dispatcher.
• the context can be represented as a structure (note: a union can be used to simplify the analysis in IDA when the context elements are dynamically accessed):

struct ctx_struct {
  uint32_t _r0;
  uint32_t _r1;
  uint32_t _r2;
  uint32_t _r3;
  uint32_t _r4;
  uint32_t _r5;
  uint32_t _r6;
  uint32_t _r7;
  uint32_t _r8;
  uint32_t _r9;
  uint32_t _r10;
  uint32_t _r11;
  uint32_t _r12;
  uint32_t _r13;
  uint32_t _r14;
  uint32_t _r15;
  uint32_t table[48];
};
union ctx_t {
  struct ctx_struct _struct;
  uint32_t addr[64];
};

Finally, there are a few conditions that must be met to get the flag:

• at the end of the XOR_REGISTERS_BLOCK + DEC_COUNTER_BLOCK loop, we must have R0 = 0xdeadbeef to access the CHECK_FLAG_BLOCK block.
• at the end of the second call to TRANSFORM_TABLE_BLOCK, we must have ctx.tab[-1] = 0xa3efa1d to get the flag.

Stage 1 - Moving 0xdeadbeef to R0

According to our analysis of the basic blocks, we know that R0 is updated by the XOR_REGISTERS_BLOCK block and depends on the values of the next registers (R1-R10). We also know that the value of the registers R5 and R6 is based on the values of the user’s arguments. Let’s analyze how our arguments are actually stored in the context:

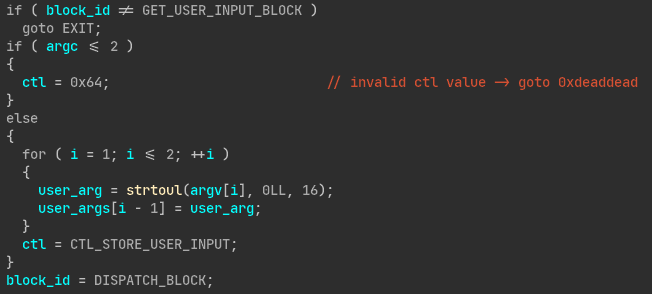
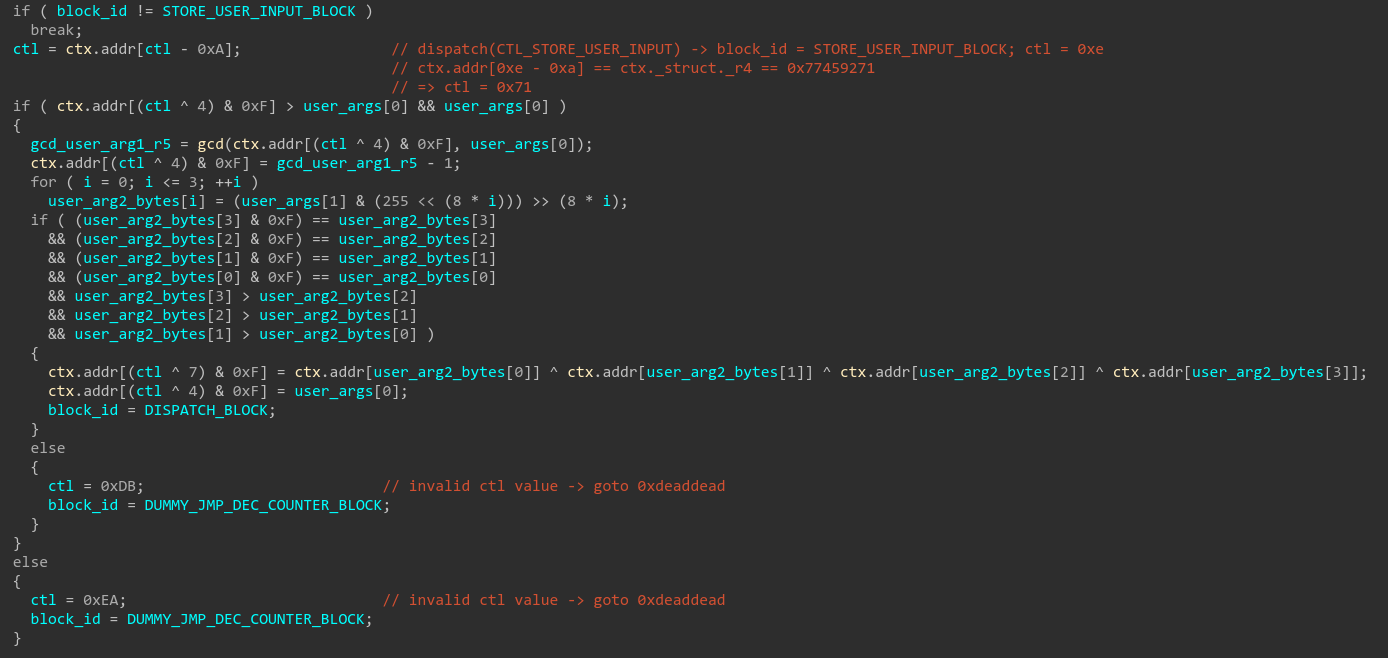
Here are the enums used in the function:

enum CTL_VALUE {
  CTL_DISPATCH = 0x0,
  CTL_TRANSFORM_TABLE = 0x13,
  CTL_DEC_COUNTER = 0x24,
  CTL_STORE_USER_INPUT = 0x42,
  CTL_DUMMY_JMP_DEC_COUNTER = 0x68,
  CTL_PREPARE_COUNTER = 0x71,
  CTL_XOR_REGISTERS = 0x79,
  CTL_GET_USER_INPUT = 0x82,
};

enum BLOCK_ID {
  DUMMY_JMP_DEC_COUNTER_BLOCK = 0x66CBBA27,
  TRANSFORM_TABLE_BLOCK = 0x679DFCE7,
  DISPATCH_BLOCK = 0x6A09E667,
  XOR_REGISTERS_BLOCK = 0x6AC7A3A7,
  PREPARE_COUNTER_BLOCK = 0x6CA7AFA7,
  GET_USER_INPUT_BLOCK = 0x6DF725A7,
  DEC_COUNTER_BLOCK = 0x70B9D067,
  STORE_USER_INPUT_BLOCK = 0x78B38527,
  CHECK_FLAG_BLOCK = 0xDEADBEEF,
  INVALID_BLOCK = 0xDEADDEAD,
};

Note: the valid values for ctl were found by reimplementing the DISPATCH_BLOCK in Python:

import idc
import idautils
import ida_allins

basic_blocks = {
    0x6a09e667: 0x137d,
    0x679dfce7: 0x13eb,
    0x6df725a7: 0x14ff,
    0x78b38527: 0x156a,
    0x6ca7afa7: 0x17b7,
    0x6ac7a3a7: 0x17d1,
    0x66cbba27: 0x1841,
    0x70b9d067: 0x184d,
    0xdeadbeef: 0x1881,
    0xdeaddead: 0x18d9
}

def ror(x, n, bits = 32):
    mask = (2**n) - 1
    mask_bits = x & mask
    return (x >> n) | (mask_bits << (bits - n))

def rol(x, n, bits = 32):
    return ror(x, bits - n, bits)

def s0(x):
    return ror(x, 7) ^ ror(x, 18) ^ (x >> 3)

def s1(x):
    return ror(x, 17) ^ ror(x, 19) ^ (x >> 10)

def e0(x):
    return ror(x, 2) ^ ror(x, 13) ^ ror(x, 22)

def e1(x):
    return ror(x, 6) ^ ror(x, 11) ^ ror(x, 25)

def ch(x, y, z):
    return z ^ (x & (y ^ z))

def dispatch(ctl):
    x = 0x6a09e667
    y = ctl
    y = (y ^ e1(0x63 ^ x ^ ((x >> 6) | (x << 2)))) % 64
    x ^= s0(ror(((ctl >> 7) | (ctl << 1)) ^ ((ctl >> 6) | (ctl << 2)), 8))
    return x

def get_block_name(id):
    return idc.get_enum_member_name(idc.get_enum_member(idc.get_enum('BLOCK_ID'), id, 0, 0))

enum = idc.add_enum(-1, 'CTL_VALUE', idaapi.hex_flag())
for ctl in range(0xff):
    block_id = dispatch(ctl)
    if block_id in basic_blocks:
        enum_mem_name = 'CTL_' + get_block_name(block_id).rstrip('_BLOCK')
        idc.add_enum_member(enum, enum_mem_name, ctl, -1)
        print(f'{enum_mem_name} = {ctl:#x}')

After a deep analysis of the STORE_USER_INPUT block, we come up with the following pseudo-code:

/* initial context values:
   ctx.r4 = 0x77459271
   ctx.r5 = 0xf7526d47
   ctx.r6 = 0x7c039e7b */
ctx = {...}

/* get user args */
user_arg1, user_arg2 = argv[1:2]

/* reset r5 value */
if user_arg1 > 0 && user_arg1 < ctx.r5:
	ctx.r5 = gcd(ctx.r5, user_arg1) - 1
else:
	exit()

/* user arg2 bytes must be different from each other
   and sorted in a descending order */
user_arg2_bytes = get_bytes(user_arg2)
if sorted(user_arg2_bytes, reverse=True) == user_arg2_bytes:
	ctx.r6 = xor([ctx[x % 16] for x in user_arg2_bytes])
	ctx.r5 = user_arg1
else:
	exit()

Looking at the pseudo-code, we understand that the bytes of the second user argument are used to reference existing register values that will be xored to each other, then, the result will be stored in R6. The first user argument is not modified and is stored in R5.

Before these assignments, we can see that R5 is reassigned to contain the greatest common divisor of R5 and the the first user argument. The analysis of the initial value of R5 (0xf7526d47) shows that it’s a prime number so the return value of gcd will always be 1: it’s probably an opaque predicate.

Here is a primality check using openssl:

openssl prime $((0xf7526d47))
F7526D47 (4149374279) is prime

We can now assume that we should be able to find a set of value for the user arguments that will give us 0xdeadbeef in R0. Let’s go ahead and try to validate the last condition allowing us to get the flag!

Stage 2 - Getting 0xa3efa1d in the context table

At first glance, the code of the TRANSFORM_TABLE_BLOCK block seems relatively simple, but when it comes to describing an expression for each cell of the table, the complexity quickly explodes:

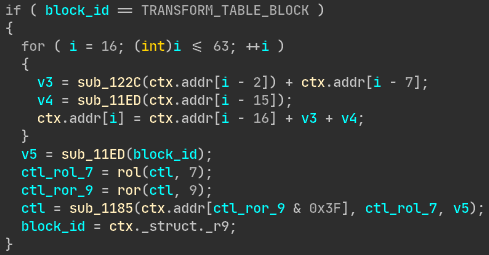
Assuming that the code was not designed by the challenge author, I looked for a simplified version of this code that would allow us to compute a preimage to get the expected value in the last cell of the table. I eventually found this code (using grep.app):

/* snippet from: https://github.com/git/git/blob/master/sha256/block/sha256.c#L72-L74 */
static void blk_SHA256_Transform(blk_SHA256_CTX *ctx, const unsigned char *buf) {
    uint32_t W[64];
	int i;
    /* ... */

    /* fill W[16..63] */
	for (i = 16; i < 64; i++)
		W[i] = gamma1(W[i - 2]) + W[i - 7] + gamma0(W[i - 15]) + W[i - 16];
    /* ... */
}

A direct comparison between this code and our program allows us to identify the use of the “Message Scheduling” stage of SHA256 hashing function in our program. This stage relies on the following functions: $$ SHR^{n}(x) = x >> n $$

$$ ROTR^{n}(x) = (x >> n) \vee (x << (32-n)) $$

$$ \Sigma _{0}^{{256}}(x) = ROTR^{2}(x) \oplus ROTR^{13}(x) \oplus ROTR^{22}(x) $$ $$ \Sigma _{1}^{{256}}(x) = ROTR^{6}(x) \oplus ROTR^{11}(x) \oplus ROTR^{25}(x) $$

$$ \sigma _{0}^{{256}}(x) = ROTR^{7}(x) \oplus ROTR^{18}(x) \oplus SHR^{3}(x) $$

$$ \sigma _{1}^{{256}}(x) = ROTR^{17}(x) \oplus ROTR^{19}(x) \oplus SHR^{10}(x) $$

Even if not all SHA256 primitives were used in the challenge code, it seems impossible to rely on an SAT solver (such as z3) to validate this part. Let’s just validate the first stage and make exhaustive tries to validate the second one.

Actual challenge solving

Here is a detailed script to solve the challenge:

import itertools
import logging

from z3 import *

log = logging.getLogger('script')
handler = logging.StreamHandler(sys.stdout)
handler.setFormatter(logging.Formatter('%(levelname)-7s | %(asctime)-8s | \x1b[33m%(message)s\x1b[0m', '%H:%M:%S'))
log.addHandler(handler)
log.setLevel(logging.DEBUG)

def ror(x, n, bits = 32):
    mask = (2**n) - 1
    mask_bits = x & mask
    return (x >> n) | (mask_bits << (bits - n))

def rol(x, n, bits = 32):
    return ror(x, bits - n, bits)

def s0(x):
    return ror(x, 7) ^ ror(x, 18) ^ (x >> 3)

def s1(x):
    return ror(x, 17) ^ ror(x, 19) ^ (x >> 10)

def xor(lst):
    x = lst[0]
    for y in lst[1:]:
        x ^= y
    return x

def transform_table(ctx, ctl):
    for i in range(16, 64):
        ctx[i] = (s1(ctx[i - 2]) + ctx[i - 7] + s0(ctx[i - 15]) + ctx[i - 16]) & (2**32) - 1
    return ctx

def solve():
    s = Solver()

    # create the context registers bitvecs.
    ctx_r = [BitVec('ctx_r%d' % i, 32) for i in range(10)]

    # create the user input bitvecs.
    inp0 = BitVec('inp0', 32)
    inp1_refs = [BitVec('inp1_refs%d' % i, 32) for i in range(4)]

    #
    # TRANSFORM_TABLE_BLOCK: transform the context table.
    #
    init_ctx = transform_table([
        # regs:
        0x1b752973, 0x8f408722, 0x5ef9e954, 0x962cd4d3, 0x77459271, 0xf7526d47, 0x7c039e7b, 0xd98f3cbf, 0xe0300990, 0x6a09e667, 0x70715969, 0x35744deb, 0xc20a3236, 0x78ddea09, 0xf4543275, 0x28a811d,
        # table:
        0x2f5af031, 0x3123cf0a, 0x8649a70d, 0x8fdf6f4b, 0xc2f3cc31, 0x7be197c2, 0xed60c0c2, 0xfefddf52, 0xd163817b, 0xfe3792ca, 0x1f7102e2, 0x5ee8cfcb, 0x2a0de01, 0x4b21e6e8, 0xede3ea57, 0xe4d1437f, 0x406d5ce, 0x960719be, 0x690465ba, 0x6d2680d8, 0xeeb64a73, 0x3abcbf76, 0x7d525c4a, 0x4ccb1655, 0xc207b2cc, 0xfd9e627f, 0x1b99c6d, 0x3cee580b, 0x4cf763e2, 0x8ce96221, 0x9e52cf92, 0x952d5764, 0x75301daf, 0xfbac726, 0x2480decd, 0x5b425d64, 0x8ba4a2b5, 0x7ce9ecb3, 0xb6f1ed16, 0xc2712e76, 0xe5431a05, 0x54bf9b7d, 0xa6354b31, 0x5487b461, 0x7f710e43, 0x46512d0d, 0x38419ddd, 0x265c408f
    ], 0x13)

    #
    # PREPARE_COUNTER_BLOCK: replace some default registers values before storing the user inputs.
    #
    init_ctx[5] = 0  # gcd(R5, user_arg_1) - 1 == 0
    init_ctx[10] = 9

    #
    # GET_USER_INPUT_BLOCK + STORE_USER_INPUT_BLOCK
    #
    # add constraints over inp1 references:
    #  * references should only refer to a register value
    #  * references should be different from each other
    for i in range(4):
        s.add(Or(*[inp1_refs[i] == ctx_v for ctx_v in init_ctx[3-i:16-i]]))
        for j in range(4):
            if i != j:
                s.add(inp1_refs[i] != inp1_refs[j])

    # store the user inputs into a new context containing symbolic constraints.
    final_ctx = copy.copy(init_ctx)  # keep a copy of the initial context to print solution.
    final_ctx[5] = inp0
    final_ctx[6] = xor(inp1_refs)

    #
    # XOR_REGISTERS_BLOCK + DUMMY_JMP_DEC_COUNTER_BLOCK + DEC_COUNTER_BLOCK
    #
    for i in range(9, -1, -1):
        s.add(ctx_r[i] == xor(final_ctx[i:11]))

    # save results into the final context.
    for i in range(10):
        final_ctx[i] = ctx_r[i]

    # make sure we'll be dispatched to the 0xdeadbeef block.
    s.add(ctx_r[0] == 0xdeadbeef)

    # final context state before calling TRANSFORM_TABLE_BLOCK.
    final_ctx[9] = 0xdeadbeef  # saved ip
    final_ctx[10] = 0          # counter (null)

    #
    # such a thing doesn't work... let's just SAT the first stage
    # and make exhaustive tries over concrete values for the second one.
    #
    # s.add(transform_table(final_ctx, 0x13)[63] == 0xa3efa1d)

    solve_count = 0
    while s.check() == sat:
        m = s.model()

        # get context values from model.
        final_ctx_v = list()
        for i, final_ctx_elt in enumerate(final_ctx):
            if isinstance(final_ctx_elt, BitVecRef):
                v = m[final_ctx_elt].as_long()
            else:
                v = final_ctx_elt
            final_ctx_v.append(v)

        # get input0 value from model.
        inp0_v = m[inp0].as_long()

        # get input1 references from model and
        # reverse sort them based on their context index.
        inp1_refs_i = sorted([
            init_ctx.index(m[inp1_refs[0]].as_long()),
            init_ctx.index(m[inp1_refs[1]].as_long()),
            init_ctx.index(m[inp1_refs[2]].as_long()),
            init_ctx.index(m[inp1_refs[3]].as_long())
        ], reverse=False)

        # create the program input value.
        inp1_v = 0
        for i, ref_i in enumerate(inp1_refs_i):
            inp1_v |= ref_i << (8*i)

        # get input references values from context.
        inp1_refs_v = [init_ctx[i] for i in inp1_refs_i]

        # prevent the same combination from being reused.
        s.add(
            Or(
                inp0 != m[inp0].as_long(),
                xor(inp1_refs) != xor(inp1_refs_v)
            )
        )

        #
        # CHECK_FLAG_BLOCK
        #
        if transform_table(final_ctx_v, 0x13)[63] == 0xa3efa1d:
            solve_count += 1
            log.info(f'{inp0_v:#x} {inp1_v:#x}')
    else:
        if not solve_count:
            log.error('No solution :/')
        else:
            log.info(f'Found {solve_count} solution{"s" if solve_count > 1 else ""}!')

if __name__ == '__main__':
    log.info('Running solver.')
    solve()

Output:

INFO    | 10:19:18 | Running solver.
INFO    | 10:19:18 | 0xe302c75d 0x8070605

Let’s check our result:

# ./chall 0xe302c75d 0x8070605
Congrats!
Here is your flag: DGA{e302c75d_8070605}

Bonus: using angr to solve the challenge

After solving the challenge with z3, I figured out that it was possible to solve it using angr as long as the opaque predicate identified earlier is patched:

import angr
import argparse
import claripy
import logging

class strtoul_hook(angr.SimProcedure):
    def run(self, buf, end_ptr, base):
        strtoul_bvs = self.state.globals.get('strtoul_bvs', [])
        bv = self.state.solver.BVS(f'arg{len(strtoul_bvs)}', 64, explicit_name=True)
        strtoul_bvs.append(bv)
        self.state.globals['strtoul_bvs'] = strtoul_bvs
        return bv

class gcd_hook(angr.SimProcedure):
    def run(self, a, b):
        return 1

def main(path):
    log = logging.getLogger('script')

    # load the binary.
    p = angr.Project(path, auto_load_libs=False)
    base_addr = p.loader.main_object.mapped_base

    # hook some functions.
    p.hook_symbol('strtoul', strtoul_hook())
    p.hook(base_addr + 0x126b, gcd_hook())

    # create the initial state to start execution.
    state = p.factory.entry_state(args=[path, '123', '123'], add_options=angr.options.unicorn)

    # execute the program using symbolic execution.
    sm = p.factory.simgr(state)
    sm.explore(find=lambda s: b'Congrats' in s.posix.dumps(1))

    if len(sm.found) > 0:
        for solution_state in sm.found:
            bvs = [{'obj': bv, 'val': solution_state.solver.eval(bv)} for bv in solution_state.globals['strtoul_bvs']]
            for bv in bvs[:2]:
                log.info(f'{bv["obj"].args[0]}: 0x{bv["val"]:x}')
            solution_state.add_constraints(claripy.Or(*[bv['obj'] != bv['val'] for bv in bvs]))
    else:
        log.error('No solution :/')

if __name__ == '__main__':
    logging.getLogger('script').setLevel(logging.DEBUG)

    parser = argparse.ArgumentParser()
    parser.add_argument('binary', default='./chall', nargs='?')
    args = parser.parse_args()

    main(args.binary)

We can also check if there was an obvious bias that would make us get the good value into ctx[-1]:

solution_state.mem[0x400000+0x415C].int32_t

After ten hours of processing I never got a result, this should be enough to say that step 2 could not be solved in a reasonable time using an SAT solver.

Flag

The final flag is: DGA{e302c75d_8070605}

Happy Hacking!

Creased