RSA V

EasyCTF 2018 - Cryptography (200 pts).

EasyCTF 2018: RSA V

Event Challenge Category Points Solves
EasyCTF 2018 RSA V Cryptography 200 ¯\(ツ)/¯

Description

Bob is extremely paranoid, so he decided that just one RSA encryption is not enough. Before sending his message to Alice, he forced her to create 5 public keys so he could encrypt his message 5 times! Show him that he still is not secure… rsa.txt

TL;DR

Encrypting with RSA multiple times is just multiplying the exponent and finding the associated private key. Because e was almost as big as n, a Wiener attack was able to break the encryption.

Resolution

First thing I tried is to see if n have known factors. It doesn’t… would have been too easy 🙂

When encrypting a message using textbook RSA, we compute :

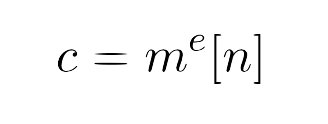
eq1.png

Where c is the ciphertext, m the plaintext converted to a number, e the public exponent and n the modulus.

Bob encrypted his message five times, so the equation is the following :

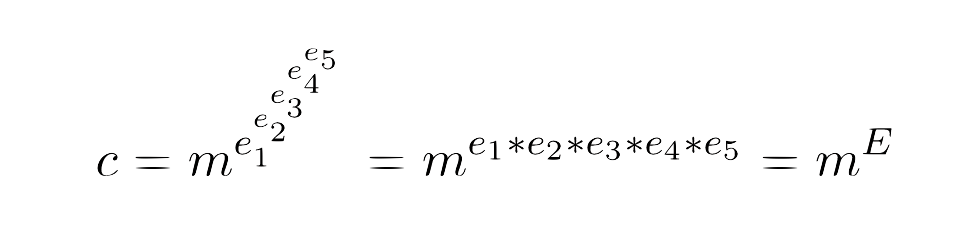
eq2.png

To recover the plaintext we don’t need to find d_1 to d_5 but only D as the decryption process is :

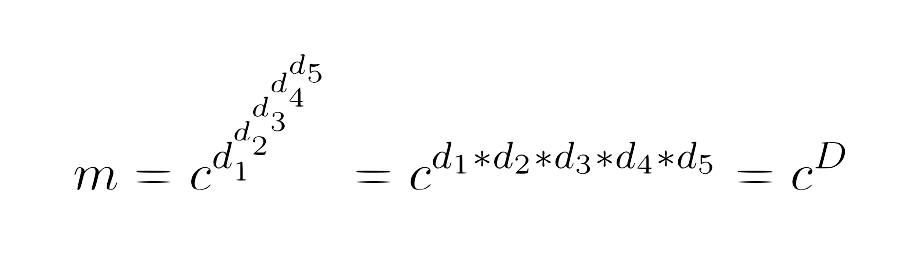
eq3.png

To recover D, we must think of an appropriate approach. First I computed E :

>>> 11*41*67623079903*5161910578063*175238643578591220695210061216092361657427152135258210375005373467710731238260448371371798471959129039441888531548193154205671
27587468384672288862881213094354358587433516035212531881921186101712498639965289973292625430363076074737388345935775494312333025500409503290686394032069L

Seeing that E is quite close to n, I decided to run a Wiener attack because the private exponent D would be relatively small compared to n. I used attackrsa for this.

$ attackrsa -t wiener -n 9247606623523847772698953161616455664821867183571218056970099751301682205123115716089486799837447397925308887976775994817175994945760278197527909621793469 -e 27587468384672288862881213094354358587433516035212531881921186101712498639965289973292625430363076074737388345935775494312333025500409503290686394032069
====== Cracked! =======
d is 0x80e51c075ffcbe945903af2e1075fb6dL
p is 0xebdd1fcde3674f5d74156a27138756718f8d51c9eae9911a3a3ac50f18019485
q is 0xbfa44dca18f4843dffeb3969cdb4e20cc0369ed1d3c2016cc12e0b3e347386d9

Bingo ! Now I got everything needed to decrypt the flag.

>>> d = 0x80e51c075ffcbe945903af2e1075fb6d
>>> c = 7117565509436551004326380884878672285722722211683863300406979545670706419248965442464045826652880670654603049188012705474321735863639519103720255725251120
>>> n = 9247606623523847772698953161616455664821867183571218056970099751301682205123115716089486799837447397925308887976775994817175994945760278197527909621793469
>>> t = pow(c,d,n)
>>> hex(t)
'0x656173796374667b6b65626c667466747a696261746473716d716f74656d6d74797dL'
>>> "656173796374667b6b65626c667466747a696261746473716d716f74656d6d74797d".decode('hex')
'easyctf{keblftftzibatdsqmqotemmty}'

Flag

The flag was easyctf{keblftftzibatdsqmqotemmty} 🙂

ENOENT